Обгрунтування господарських рішень та оцінювання ризиків – Донець Л. І. – 12.3. Змішані стратегії матричної гри
Якщо матрична гра не має сідлової точки, то використання чистих стратегій не дає оптимального рішення гри. Так матрична гра, яку розглянуто у прикладі 12.3, не має сідлової точки. В цьому випадку можна отримати оптимальне рішення, випадково обираючи чисті стратегії.
Якщо матрична гра не має сідлової точки, то виникає необхідність гри в змішаних стратегіях.

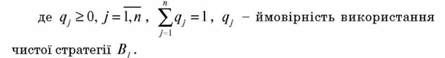
Змішані стратегії представлять математичну модель мінливої і гнучкої тактики гравця, при якій його противник не може довідатись заздалегідь про те становище, в якому йому доведеться опинитись. Перед кожною партією відбувається випадковий вибір однієї з чистих стратегій з деякою певною і вже визначеною ймовірністю.
Гравці вибирають стратегії випадково і незалежно один від одного, тому гра має випадковий характер і сума виграшу теж стає випадковою.
За принципом мінімаксу (максиміну) визначається оптимальне рішення гри – це пара оптимальних стратегій SoA, SoB в загальному випадку змішаних, які мають властивість: якщо один з гравців дотримується своєї оптимальної стратегії, то другому не може бути вигідно відступати від своєї оптимальної стратегії.
Виграш, що відповідає оптимальному рішенню гри, називається ціною гри.
Ціна гри – це об’єктивно можливий середній виграш
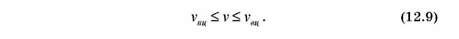
Основна теорема теорії ігор – теорема Неймана: кожна скінченна гра має хоча б одне оптимальне рішення, можливо серед змішаних стратегій.
Якщо чиста стратегія входить в оптимальну з певною ймовірністю, яка відрізняється від нуля, то вона називається активною стратегією.
Теорема про активні стратегії: якщо один із гравців дотримується своєї оптимальної змішаної стратегії, то його виграш залишиться незмінним і буде дорівнювати ціні гри, якщо другий гравець не вийде за границі своїх активних стратегій.
Зміст теореми полягає в тому, що при послідовному дотриманні одним з гравців оптимальної змішаної стратегії, то його виграш не менше ціни гри, незалежно від дій другого гравця, який не вимозі змінити результат гри.
12.4. Розв’язування матричних ігор розміру 2×2
Розглянемо матричну парну гру розміру 2×2.
Таблиця 12.9. Матрична парна гра розміру 2×2

Якщо така гра має сідлову точку, то оптимальне рішення – це пара чистих стратегій, які відповідають цій точці.
Якщо матрична гра не має сідлової точки, то основною теоремою теорії ігор вона має хоча б одне оптимальне рішення, яке

Середній виграш буде дорівнювати ціні гри V, яку б активну стратегію не використовував б гравець В. Для гри розміру 2×2 будь-яка чиста стратегія є активною, якщо сідлова точка відсутня. Виграш гравця А (програш гравця В) представляє собою випадкову величину, математичне очікування якої дорівнює ціні гри. Тому середній виграш гравця А (оптимальна стратегія) буде дорівнювати V для першої і другої стратегій гравця В.


Розв’язуючи систему (2.3.1), отримаємо значення шуканих ймовірностей

І ціни гри


Використанні будь-якої чистої стратегії гравця А середній програш гравця В дорівнює ціні гри v, тобто

Звідки отримаємо значення шуканих ймовірностей

Приклад 12.4. Знайти рішення матричної гри, платіжну матрицю якої побудовано в прикладі 12.1.
Розв язаттття. Знайдемо нижню і верхню ціни гри за допомогою алгоритму знаходження максиміну (мінімаксу). В кожному рядку платіжної матриці знайдемо мінімальне з чисел aij і запишемо його у додатковий стовпчик minaij.
Таблиця 12.10 Платіжна матриця гри про вибір сторони монети

З найдених чисел виберемо найбільше за формулою (12.5) а = max ai = max {-1,-1} = -1, що визначає нижню ціну гри або максимін, тобто максимальний виграш, який гравець А може собі гарантувати в грі, що розглядається. Цей виграш відповідає стратегіям A1, A2. Тобто кожна стратегія фірми А є максимінною.
В кожному стовпці платіжної матриці знайдемо максимальне з чисел aij запишемо його у додатковий рядок max aij.
З найдених чисел виберемо найменше за формулою (12.6) ß = min ßj = min {1,1} = 1, що визначить верхню ціну гри або мі-німакс, тобто мінімальний програш, який гравець В може собі дозволити в грі, що розглядається, який відповідає стратегіям B1, B2. Ці стратегії є мінімаксними.



Розв язання. Скоротимо розмірність платіжної матриці. Стратегії А1 і А3 гравця А співпадають, тому виключимо стратегію А3:

Стратегії В5, В3 і В2 гравця В домінують стратегію В1, тому їх можна виключити з платіжної матриці:

Стратегія А1, гравця А домінується стратегію А2, тому стратегію А1 можна виключити з платіжної матриці: